엘리엇 파동이론
파동 카운팅
이번 챕터에서는 차트에 파동을 카운팅 하기 위해 직접적으로 필요한 피보나치 비율, 파동간의 비율, 피보나치 시계열, 채널링 등에 대해 다루고 카운팅 예시들도 살펴 보도록 하겠습니다.
(1) 피보나치 수열(Fibonacci Sequence)과 비율(Ratio)
뒤에서 자세히 설명하겠지만 엘리엇 파동이론은 피보나치 수열, 비율과 깊은 관계를 가지고 있습니다. 피보나치 비율은 각 파동간의 비율을 설명하기에 이를 알면 현재 진행중인 파동을 사용하여 앞으로 나올 파동의 목표값 등을 설정할 수 있기에 유용합니다. 이는 피보나치 비율이 자연에서 빈번히 발생하는 비율이며 사람의 행동과 군중심리가 반영된 차트에서도 발생한다고 파동이론은 설명합니다. 여기서는 피보나치 비율의 정의와 그것이 자연에서 어떻게 보여지는지 살펴보겠습니다.
✅피보나치 수열(Fibonacci Sequence)
이탈리아 수학자 피보나치가 고안한 것으로 알려져 있는 피보나치 수열은 다음과 같이 정의합니다.
F(1) = 1,
F(2) = 1,
F(n) = F(n-1) + F(n-2), n = 3, 4, 5, 6, 7, 8 ….
수열(Sequence)이라는 것은 단순히 순자를 일렬로 나열해 놓은 것을 수열이라고 합니다. 위 피보나치 수열의 정의에서 F(n) 은 수열의 n 번째 숫자를 의미합니다. F(1) = 1 이라는 것은 피보나치 수열의 첫번째 숫자가 1 임을 의미하며, F(2) = 1 이라는 것은 2번째 숫자도 1임을 의미합니다. F(n) = F(n-1) + F(n-2) 는 n이 3 이상일 때는 그저 앞선 두 수의 합이 n번째 숫자가 됨을 의미합니다.
즉, 피보나치 수열은 첫번째와 두번째는 1, 이후는 앞선 두 수의 합으로 이루어진 숫자의 나열로써 다음과 같습니다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …..
이는 끝없이 이어지는 무한수열입니다. 1+1=2, 1+2=3, 2+3=5, 3+5=8 이런 식으로 앞선 두개의 숫자의 합이 다음 숫자입니다.
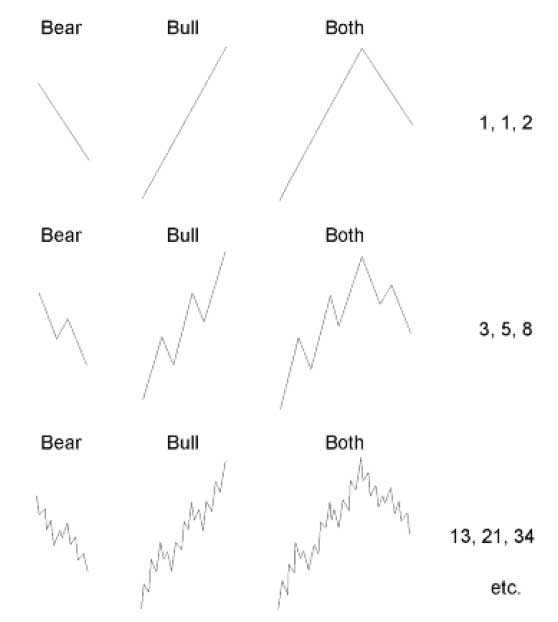
엘리엇 파동이론은 기본적으로 피보나치 수열의 구조를 가지고 있다고 이야기 하는데 그림 12-39를 보시면 파동의 개수는 피보나치 수열의 숫자를 따릅니다. 파동을 자세하게 쪼갤수록 파동의 개수는 많아지지만 피보나치 수열에서 벗어나지 않습니다.
✅피보나치 비율(Fibonacci Ratio)
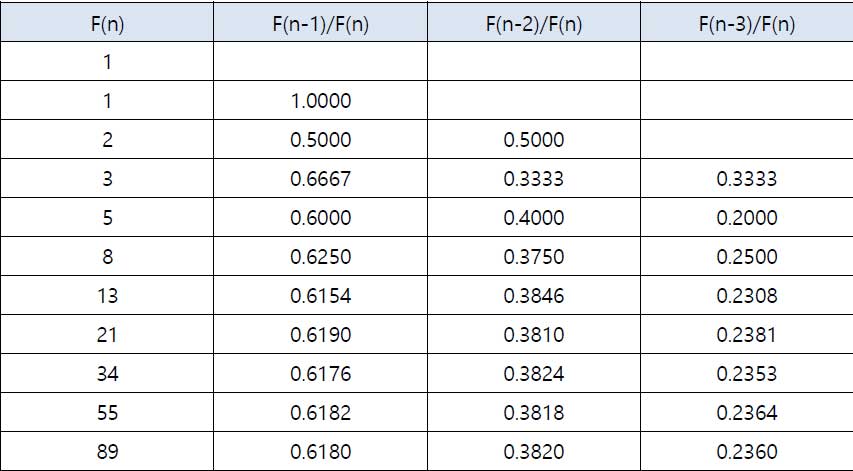
위 표의 가장 왼쪽 컬럼 F(n)은 피보나치 수열입니다. 2번째 컬럼은 피보나치 수열의 인접한 숫자들간의 비율입니다. 3번째 컬럼은 피보나치 수열에서 한 칸 건너 띈 숫자들 간의 비율이며 4번째 컬럼은 두 칸 건너 띈 숫자들 간의 비율입니다. 이 숫자들을 뒤로 갈수록 어느 숫자에 가깝게 수렴해 가는데 이 숫자들이 피보나치 비율 0.236, 0.382, 0.618 입니다.

위 표는 피보나치 비율을 1에서 뺀 값, 피보나치 비율의 역수, 피보나치 비율의 제곱근 입니다. 이 숫자들도 역시 중요한 비율로써 활용됩니다.
가장 중요한 비율은 0.618 과 0.382 이며 다음으로 1.618, 2.618, 0.236, 0.786 등이 중요합니다.
✅황금 분할(Golden Section), 황금 비율(Golden Ratio)

그림 14-40 에서 직선을 a와 b로 나누어 놓았는데 a는 0.382, b는 0.618로써 이 비율을 황금비율이라고 합니다. a+b=1 이므로 전체 길이 대비 a와 b의 비율은 0.382 와 0.618 입니다. 이러한 비율 관계들을 나열해 보면
a + b = 1
a / b = 0.618
b / a = 1.618
즉, 전체대비 a의 비율인 0.382, 전체 대비 b의 비율인 0.618, a대비 b의 비율인 1.618 모두 사실 같은 비율 관계임을 알 수 있습니다. 이러한 비율들을 황금비율(Golden Ratio)이라 하며 황금 비율로 쪼개 놓은 것을 황금분할(Golden Section)이라 합니다.
✅황금 직사각형(Golden Rectangular)
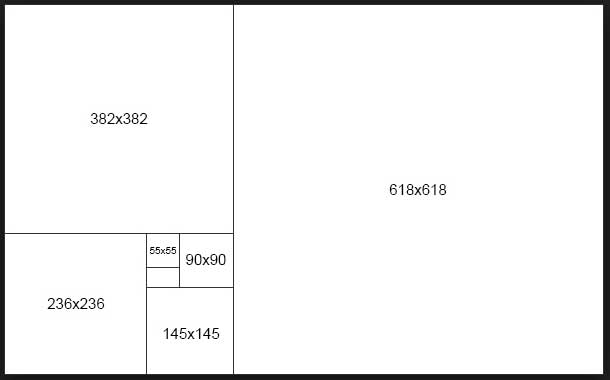
그림 12-41의 사각형이 황금 직사각형입니다. 가장 큰 사각형(테두리)의 가로변과 세로변은 0.618의 황
금비율을 이룹니다. 여기서 가로변을 0.382 : 0.618 로 분할하면 정사각형 하나와 직사각형 하나가 만들어지는데 이 직사각형도 각 변의 비율이 0.618의 황금 직사각형이 됩니다. 이를 다시 황금비율로 쪼개면 정사각형 하나와 직사각형 하나가 만들어지는데 이 직사각형 또한 황금 직사각형이 됩니다. 이는 무한히 반복할 수 있습니다.
✅황금 나선(Golden Spiral)
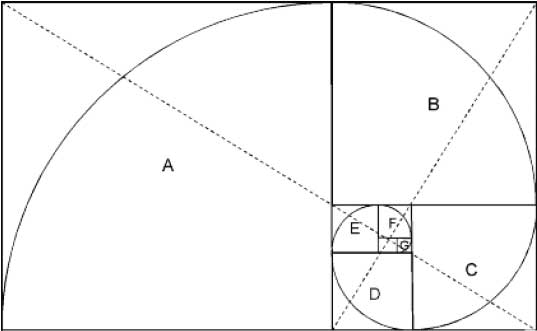
황금 직사각형의 각 정사각형 들에 원호을 그려 넣으면 위 점선들이 교차하는 점을 중심으로 나선형의 그림을 그릴 수 있는데 이를 황금 나선이라 합니다. 이는 무한히 반복될 수 있습니다.
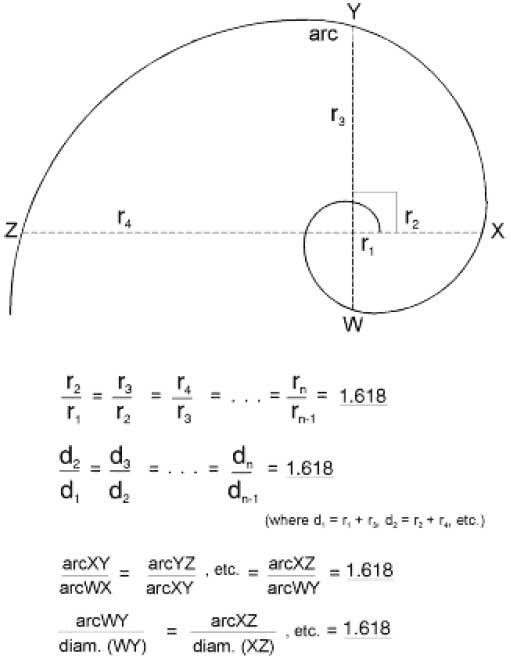
그림 12-43과 같이 황금 나선은 그 지름, 반지름, 호 등의 비율 관계가 1.618 황금비율을 이룹니다.
✅자연의 법칙(Law of Nature)
앞서 설명한 황금 비율과 황금 분할, 황금 나선 등은 자연계에서 빈번하게 나타납니다.


유전자 구조에서부터 파도의 모양, 태풍의 모양, 꽃, 달팽의 껍질, 은하의 나선 팔에 이르기까지 황금 비율과 황금나선 구조가 나타나는 예는 무수히 많습니다.
황금 비율이 우주의 근본 원리라고 주장하는 것은 과장일 수도 있겠지만 파도나 은하와 같은 동역학적인 움직임에서 나타나며 중앙에서부터 퍼져나가는 혹은 중앙으로 퍼져나가는 양뿔이나 꽃잎, 달팽이 껍질 등에서 나타난다는 것은 이것이 자연계에서 선호하는 비율이며 생성과 진행, 또는 후행과 퇴보시에 자연계에서 발생하는 패턴이라는 것은 이야기 할 수 있을 것 같습니다.
인간 또한 대자연(Nature)의 일부로써 인간의 행동 패턴 혹은 심리에도 이와 같은 황금비율이 녹아 있다고 주장한다면 과장이라 할 수도 있겠지만 그 근거로 들만한 것들이 있습니다.

자연계에서 피보나치 비율이 많이 등장하지만 인간이 창조한 고대부터의 예술작품 속에서도 황금비율, 황금분할 등은 여러 곳에서 찾아볼 수 있습니다. 인간은 황금비율을 아름답게 느끼고 그 속에서 안정을 찾을 수 있는 것으로 알려져 있습니다. 그것이 미학적으로 혹은 생리적으로 어떠한 구체적인 작용에 의해 발생한다고 말하긴 어렵더라도 인간의 심리에 이미 피보나치 비율이 녹아 있다고 주장하는 것은 억지일까요?
엘리엇 파동이론에서는 이와 같은 대자연의 원리인 피보나치 비율이 파동 크기의 비율과 시간관계에서도 나타난다고 주장하고 있습니다. 물론 항상 지켜지는 것은 아니지만 무시하기에는 빈번하게 발생하며 정확하지 않더라도 일정한 범주 안에 들어 있는 경우가 많기에 알아둘 필요가 있습니다.

